科学研究

       交替方向法是一种典型的一阶优化方法，在机器学习、统计学习、图像处理等领域有着广泛的应用。近年来，受到人工智能和大数据的驱动，随机交替方向法成为研究热点。然而现阶段的随机交替方向法把原始-对偶变量均放在一个内循环中，且学习率为固定值1，这在一定程度上削弱了算法的数值性能。

       本工作打破现有随机交替方向法的设计思路，仅把光滑子问题的求解放在一个内循环中，发展了一种理论上收敛的非精确加速随机交替方向法（简称AS-ADMM）。具体而言，针对一类含有限和目标的可分离凸优化模型，设计了一种基于小批量样本和动量加速技术的AS-ADMM。随后，将该方法推广至带较大学习率的对称AS-ADMM（简称SAS-ADMM）以及局部并行(或串行)求解的多分块AS-ADMM。利用变分不等式框架，系统建立了算法在期望意义下的次线性收敛速度理论。特别的，在强凸假设下还建立了算法关于迭代点列的线性收敛速度理论。最后，通过调用LIBSVM网站上的公开数据集验证了所提算法求解监督学习问题的高效性，部分对比实验结果如下图所示。

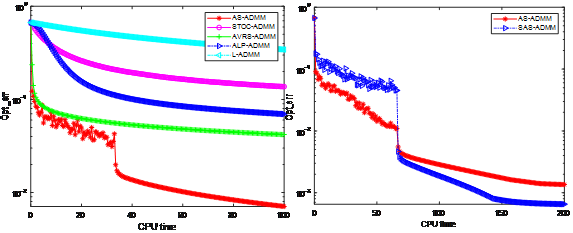
       本项工作由西北工业大学白建超、北京航空航天大学韩德仁等人合作完成，且第一作者白建超受邀分别在河南省运筹学会2021年学术年会和陕西省运筹学会2022年学术年会上做了大会特邀报告。

       与本成果相关的论文：[1]J. Bai,W. Hager,H. Zhang. An inexact accelerated stochastic ADMM for separable composite convex optimization, Computational Optimization and Applications, 81 (2022), 479-518. [2]J. Bai, D. Han, H. Sun, H. Zhang. Convergence analysis of an inexact accelerated stochastic ADMM with larger stepsizes,Publishedonline in CSIAM Transactions on Applied Mathematics, (2022), DOI:10.4208/csiam-am.SO-2021-0021.

       图/文：张硕  审稿人：徐根玖